五年级华杯赛试题
时间:2021-08-31华杯赛是为了纪念我国杰出数学家华罗庚教授,于1986年始创的全国性大型少年数学竞赛活动,下面小编为大家带来五年级华杯赛试题,希望对大家有帮助!
五年级华杯赛试题一
一、选择题(每小题10分)以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内.
1、在1至300的全部自然数中,是3的倍数或5的倍数的数共有( )个。
A、139 B、140 C、141 D、142
2、甲每分钟走55米,乙每分钟走75米,丙每分钟走80米。甲、乙两人同时从A地,丙一人从B地同时相向出发,丙遇到乙后4分钟又遇到甲,则A地与B地间的距离是( )。
A、4000米 B、4200米 C、4185米 D、4100米
3、对所有的数a,b,把运算a*b定义为a*b=ab-a+b,则方程5*x=17的解是( )。
A、523 B、2 C、3 D、3
4、植树节到了,某市举行大型植树活动,共有1430人参加植树,要把人数分成相等的若干队,且每队人数在100至200之间,则有分法( )。
A、3种 B、7种 C、11种 D、13种
5、如图,已知正方形ABCD的边长是12厘米,E是CD边上的中点,连接对角线AC,交BE于点O,则三角形AOB的面积是( )平方厘米。
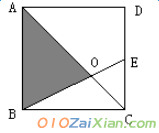
A、24 B、36 C、48 D、60
6、下图有九个空格,要求每个格中填入互不相同的数,使得每行、每列、每条对角线上的三个数之和都相等,则图中左上角的数是( )。
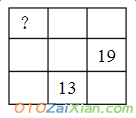
A、9 B、16 C、21 D、23
二、填空题(每小题10分).
7、有一种饮料的瓶身如下图所示,容积是3升。现在它里面装了一些饮料,正放时饮料高度为20厘米,倒放时空于部分的高度为5厘米。那么瓶内现有饮料 升。
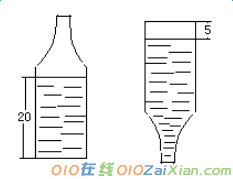
8、在一次“人与自然”知识竞赛中,竞赛试题共有25道题。每道题都给出4个答案,其中只有一个答案正确,要求学生把正确答案选出来。每道题选对得4分,不选或选错倒扣2分。 如果一个学生在本次竞赛中的得分要不低于60分,那么,他至少要选对 __________道题。
9、某超市从厂家以每件21元的价格购进一批商品,该超市可以自行定价,但物价局限定每件商品加价不能超过售价的20%,则这批商品的售价不能超过____________元。
10、小刚骑车从8路汽车的起点站出发,沿着8路车的行驶路线前进。当他骑了1650米时,一辆8路公共汽车从起点站出发,每分钟行450米。这辆汽车在行驶过程中每行5分钟停靠一站,停车时间为1分钟。已知小刚骑车速度是汽车行驶速度的3/2,则这辆汽车出发后要追上小刚需要时间 分钟。
答案:
BCDACB
2.4、19、26.25、17
五年级华杯赛试题二
一、选择题:
1、一个双层书架,上层书的本数是下层书的5倍。如果从上层搬80本到下层,那么两层书的本数正好相等。原来上、下层各有图书多少本?
A.下层16本,上层80本 B. 下层20本,上层100本
C. 下层40本,上层200本 D、下层30本,上层150本
2、A、B两船共载客623人,若A船增加34人,B船减少57人,这时两船乘客同样多,A船原有乘客( )人。
A、266 B、357 C、300 D、350
3、由1、2、3、4、5五个数字组成的五位数有120个,将它们从大到小排列起来,第95个数是( )。
A、51234 B、31254 C、41253 D、21354
4、已知除法算式中,被除数、除数、商和余数相加得2011,当除数为一位数,余数为6时,被除数是( )。
A、1797 B、1598 C、1399 D、1199
二、填空题:
1、将一个三位数末两位数字交换位置后得到一个新的三位数,这个新三位数与原三位数的和是一个四位数A73B,那么,符合上述条件的原三位数共有 个。
2、 2000+1999-1998-1997+1996+1995-1994-1993++8+7-6-5+4+3-2-1= 。 3、(国富+民富)×强强=2002,算式中的“国富”“民富”“强强”表示3个两位数,相同的汉字代表相同的数字,不同的汉字代表不同的数字。“国、富、民、强”所代表的四个数的和是 。
4、甲、乙、丙三人的.钱数各不相同。甲最多,他拿出一些给乙和丙,使乙和丙的钱数都比原来增加两倍,结果乙的最多;乙再拿出一些给甲和丙,使甲和丙的钱数比原来增加两倍,结果丙最多;丙又拿出一些给甲和乙,使他们的钱数各增加两倍,结果三人的钱数一样多。如果他们三人共有81元,则三人原来的钱分别是 、 、 。
三、解答题:
1、小丽在计算一道求7个自然数的平均数(得数保留两位小数)时,将得数的最后一位算错了,她的错误答案是21.83。正确答案是多少? 2、某校人数是一个三位数,平均每个班级36人,若将全校人数的百位数字与十位数字对调,则全校人数比实际少180人,那么该校人数最多可达到多少人?
3、甲、乙两人进行百米赛跑,当甲到达终点时,乙在甲后面20米处;如果两人各自的速度不变,要使甲、乙两人同时到达终点,甲的起跑线应比原起跑线后移多少米?
如下图所示,正方形与阴影长方形的边平行,正方形边长为10,阴影长方形的面积为6,那么图中四边形ABCD的面积是多少?
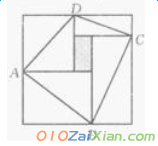
【五年级华杯赛试题】相关文章:
1.华杯赛初赛试题
4.华杯赛试题练习











