平面向量基本定理与线性规划教学设计和反思

　　【教材分析】

　　向量坐标化使平面向的学习代数化，难度降低了很多。但学生对平面向量基本定理的应用还是不太熟练，特别是由变量求范围问题，更是一头雾水。所以专门安排了这一节课来突破这个难点。

　　【学生分析】

　　经过了一轮复习的高三学生，对于向量的坐标运算、平面向量基本定理、和线性规划这些知识点的单独学习已经掌握得不错，但对于解决有范围或求最值时的平面向量基本定理的.应用还是比较棘手，所以需要老师能够由浅人深地讲解突破。难度很高。

　　【学习目标】

　　理解平行四边形法则和线性规划

　　掌握平向量基本定理的应用

　　【教学策略】

　　特殊和一般的类比学习，线性规划解决最值范围问题的策略渗透

　　【教学过程】

　　【引题】

　　【例题】1.

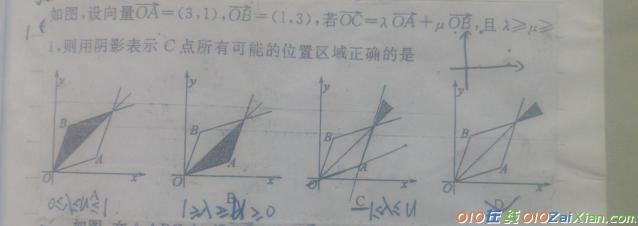
　　2.已知点

　　,平面区域D是由所有的满足

　　的点P(x,y)组成的区域，若区域Ｄ的面积为 8，则4a+b的最小值为 。

　　【练习】

　　1.已知向量

　　,设

　　。求动点P轨迹形成的图形的面积?

　　已知

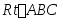
　　中，AB=3,BC=4,AC=5，I是

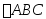
　　的内心，P是

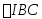
　　内部（不含边界）的动点，若

　　,则

　　的范围是 。

　　教学反思

　　总体来说本节课成功地完成了教学任务，突破了难点，学习了重点，教学效果良好。

　　但也有很多值得改进的地方，比如前面知识的讲解虽然效果不错，但也有时间的浪费，还可以省下5分钟，板书稍显混乱，可以耿耿整洁，这一点后来做得很好。

【平面向量基本定理与线性规划教学设计和反思】相关文章：

1.《平面向量基本定理》教案

2.平面向量基本定理的教学反思范文

3.平面向量教学反思

4.《平面向量基本定理及坐标表示》评课稿

5.高三平面向量教学反思

6.平面向量的基本定理及坐标表示的说课稿

7.平面向量说课课件

8.平面向量教学课件