反比例函数知识点总结
时间:2021-08-31各位同学们注意啦,小编给大家带来了反比例函数知识点总结,下面贴出内容,希望大家喜欢。
反比例函数知识点总结
若k为常数,则函数y=k/x就是反比例函数,自变量和自变量的函数分别是x和y,又因为反比例函数式本身是一个分数,所以x可以是任意不等于0的实数。同时,函数式有时候也写成y=k·x^(-1)或者k=xy.反比例和正比例函数以及一次函数等都是二次函数的基础,它们的应用一样广泛,所以不要轻视反比例函数。
那么,怎样学好反比例函数?其实反比例函数不难,只要能理清思路,把反比例函数知识点理清,把反比例函数图像理解透彻,一切是那么容易,总之,只要你能熟练数形结合,任何函数学习都会轻松很多。
步骤/方法以下是反比例函数知识点总结
1、反比例函数的表达式
X是自变量,Y是X的函数
y=k/x=k·1/x
xy=k
y=k·x^(-1)(即:y等于x的负一次方,此处X必须为一次方)
y=kx(k为常数且k≠0,x≠0)若y=k/nx此时比例系数为:k/n
2、函数式中自变量取值的范围
①k≠0;②在一般的情况下,自变量x的取值范围可以是不等于0的任意实数;③函数y的取值范围也是任意非零实数。
解析式y=k/x其中X是自变量,Y是X的函数,其定义域是不等于0的一切实数
y=k/x=k·1/x
xy=k
y=k·x^(-1)
y=kx(k为常数(k≠0),x不等于0)
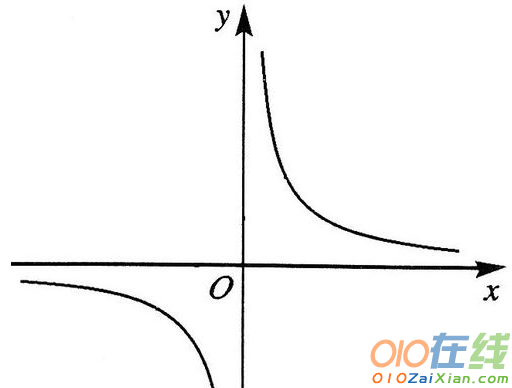
3、反比例函数图象
反比例函数的图像属于以原点为对称中心的中心对称的双曲线(hyperbola),
反比例函数图像中每一象限的每一支曲线会无限接近X轴Y轴但不会与坐标轴相交(K≠0)。

4、反比例函数中k的几何意义是什么?有哪些应用?
过反比例函数y=k/x(k≠0),图像上一点P(x,y),作两坐标轴的.垂线,两垂足、原点、P点组成一个矩形,矩形的面积S=x的绝对值*y的绝对值=(x*y)的绝对值=|k|
研究函数问题要透视函数的本质特征。反比例函数中,比例系数k有一个很重要的几何意义,那就是:过反比例函数图象上任一点P作x轴、y轴的垂线PM、PN,垂足为M、N则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。
所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数。从而有k的绝对值。在解有关反比例函数的问题时,若能灵活运用反比例函数中k的几何意义,会给解题带来很多方便。
5、反比例函数性质有哪些?
1.当k>0时,图象分别位于第一、三象限,同一个象限内,y随x的增大而减小;当k<0时,图象分别位于二、四象限,同一个象限内,y随x的增大而增大。
2.k>0时,函数在x<0上同为减函数、在x>0上同为减函数;k<0时,函数在x<0上为增函数、在x>0上同为增函数。定义域为x≠0;值域为y≠0。
3.因为在y=k/x(k≠0)中,x不能为0,y也不能为0,所以反比例函数的图象不可能与x轴相交,也不可能与y轴相交。
4.在一个反比例函数图象上任取两点P,Q,过点P,Q分别作x轴,y轴的平行线,与坐标轴围成的矩形面积为S1,S2则S1=S2=|K|
5.反比例函数的图象既是轴对称图形,又是中心对称图形,它有两条对称轴y=xy=-x(即第一三,二四象限角平分线),对称中心是坐标原点。
6.若设正比例函数y=mx与反比例函数y=n/x交于A、B两点(m、n同号),那么AB两点关于原点对称。
7.设在平面内有反比例函数y=k/x和一次函数y=mx+n,要使它们有公共交点,则n^2+4k·m≥(不小于)0。
8.反比例函数y=k/x的渐近线:x轴与y轴。
9.反比例函数关于正比例函数y=x,y=-x轴对称,并且关于原点中心对称.
10.反比例上一点m向x、y分别做垂线,交于q、w,则矩形mwqo(o为原点)的面积为|k|
11.k值相等的反比例函数重合,k值不相等的反比例函数永不相交。
12.|k|越大,反比例函数的图象离坐标轴的距离越远。
13.反比例函数图象是中心对称图形,对称中心是原点
【反比例函数知识点总结】相关文章:
1.反比例函数说课稿
3.反比例函数k课件
6.反比例函数练习题











