导语：函数指一个量随着另一个量的变化而变化，或者说一个量中包含另一个量。以下是初中函数练习题及答案的内容，仅供参考学习。

　　初中函数练习题及答案

　　一、选一选，慧眼识金（每小题3分，共２４分）

　　1．下列函数关系式：①,y=-2x ② y=-2/x ,  ③y=-2x2, ④y=2 ,  ⑤y=2x-1.其中是一次函数的是                                                     （  ） （Ａ）①⑤          （Ｂ）①④⑤

　　（Ｃ）②⑤             （Ｄ）②④⑤

　　2．一个正比例函数的图象经过点（2，-1），那么这个正比例函数的表达式为     （  ）

　　（Ａ）y=2x         （Ｂ）y=-2x

　　（Ｃ）xy21         （Ｄ）xy2 1

　　３．函数y=-3x-6中，当自变量x增加１时，函数值y就           （ ）

　　（Ａ）增加３    （Ｂ）减少３

　　（Ｃ）增加１     （Ｄ）减少１

　　４.在同一直角坐标系中，对于函数：①y=-x-1   ②y=x+1    ③y=-x+1  ④y=-2(x+1)的图象，下列说法正确的是                  （） （Ａ）通过点（－１，０）的是①和③     （Ｂ）交点在y轴上的是②和④

　　（Ｃ）互相平行的是 ①和③             （Ｄ）关于x轴平行的是②和③

　　５．一次函数y=-3x+6的图象不经过                    （ ）

　　（Ａ）第一象限  （Ｂ）第二象限

　　（Ｃ）第三象限   （Ｄ）第四象限

　　６．已知一次函数y=ax+4与y＝bx-2的图象在x轴上交于同一点，则a b 的值为   （ ）

　　（Ａ）４     （Ｂ）－２

　　（Ｃ）-2/1     （Ｄ）2/1

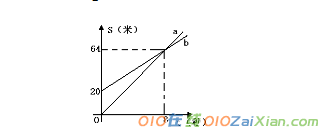
　　７．小明、小强两人进行百米赛跑，小明比小强跑得快，  如果两人同时跑，小明肯定赢，现在小明让小强先跑若 干米，图中的射线a、b分别表示两人跑的路程与小明 追赶时间的关系，根据图象判断：小明的速度比小强的 速度每秒快

　　A、1米  B、1.5米

　　C、2米  D、2.5米

　　８．如图中的图象（折线ABCDE）描述了一汽车在某一直线 上的行驶过程中，汽车离出发地的距离s（千米）和行驶时 间t（小时）之间的函数关系，根据图中提供的信息，给出 下列说法：①汽车共行驶了120千米；②汽车在行驶途中停 留了0.5

　　小时；③汽车在整个行驶过程中的平均速度为 3 80 千米/时；④汽车自出发后3小时至4.5小时之间行驶的速度 在逐渐减少.其中正确的说法共有（      ）

　　A、1个   B、2个

　　C、3个      D、4个

　　二、填一填,画龙点睛(每小题 4分,共32分)

　　1．某种储蓄的月利率为0.15%，现存入1000元，则本息和y（元）与所存月数x之间的函数关系式是                       .

　　2. 一次函数y= -2x+4的图象与x轴交点坐标是         ，与y轴交点坐标是          与坐标轴围成的三角形面积是        。

　　3．下列三个函数y= -2x,  y= - 14 x,   y=(2 - 3 )x共同点是（1）              ;  （2）                      ;（3）                     .

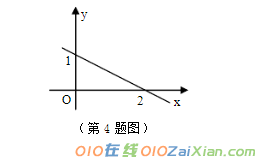
　　4．如图，直线m对应的函数表达式是。

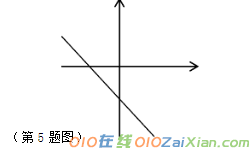
　　5．一次函数y=kx+b的图象如图所示，则k      0,b     0( 填“>”、“=”或 “<”)

　　6．写出同时具备下列两个条件的一次函数表达式（写出一个即可）                .

　　（1）y随着x的增大而减小。

　　（2）图象经过点（1，-3）

　　7．某人用充值50元的IC卡从A地向B地打长途电话，按通话时间收费，3分钟内收费2.4元，以后每超过1分钟加收1元，若此人第一次通话t分钟（3≤t≤45），则IC卡上所余的费用y（元）与t（分）之间的关系式是          .

　　8.如图，已知A地在B地正南方3千米处，甲乙两人同时分    别从A、B两地向正北方向匀速直行，他们与A地的距离S（千米）与所行的时间t（小时）之间的函数关系图象如图所示的AC和BD给出，当他们行走3小时后，他们之间的`距离为             千米.

　　三、做一做，牵手成功（本大题共64分）

　　1．(9)为了保护学生的视力，课桌椅的高度都是按一定的关系配 套设计的。研究表明，假设学生的课桌高度为y（㎝）,椅子的高度（不含靠背）为x（㎝），则y 应是x的一次函数。下表列出两 套符合的课桌椅的高度：

　　２、(9)随着我国人口增长速度的减慢，小学入学儿童数量有所减少．下表中的数据近似地呈现了某地区入学儿童人数的变化趋势．

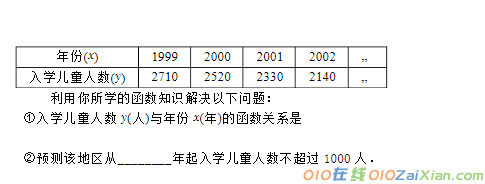
　　３、(9)在某地，人们发现某种蟋蟀1分钟所叫次数与当地温度之间近似为一次函数关系。

　　下面是蟋蟀所叫次数与温度变化情况对照表：

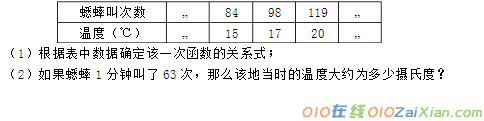
　　４．(9)旅客乘车按规定可携带一定重量的行李，如果超过规定则需购行李票，设行李费y（元）是行李重量x（千克）的一次函数，其图象如图所示。 （1）求y与x之间的函数关系式；  （2）旅客最多可免费携带多少千克行李？

　　５．(14)已知某一次函数的图象经过点(0, -3),且与正比例函数y= 12 x的图象相交于  点(2，a),求     （１）  a的值。 （２）k、b的值。  （３）在同一直角坐标系中画出这两个函数的图象。 （４）这两个函数图象与x轴所围成的三角形面积。

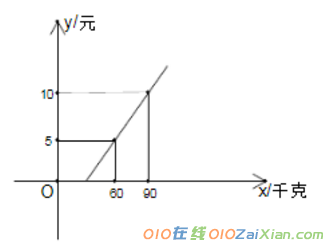
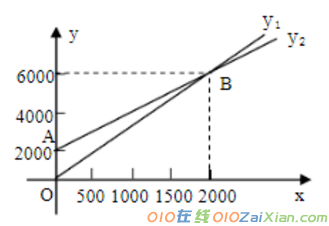
　　6．(14)某单位急需用车，但又不需买车，他们准备和一个个体车或一国营出租公司中的一家签订月租车合同。设汽车每月行驶x千米，应付给个体车主的月租费为y1 元，应付给国 营出租公司的月租费为y2 元，y1 、y2 与x之间的函数关系（两条射线）如图所示，观察图 象回答下列问题：  （1）每月行驶路程在什么范围内时，租用国营 出租公司的车合算？  （2）每月行驶路程是多少时，两家的费用相同？ （3） 每月行驶在什么范围内时，租用个体车合算？ （4） 这个单位估计每月行驶的路程在2300千米 左右，则租用哪家车合算？

　　答案：

　　第一题：（１—８）A、D、B、C、C、C、D、A

　　第二题：  １、ｙ＝１.5ｘ＋1000

　　2、（2，0）（0，4）、4

　　3、都是正比例函数；都过二、四象限；y都随x的增大而减小；

　　4、y=－12  x+1

　　5、<；<

　　6、y＝－x－2（符合即可）

　　7、y＝50.6-t

　　8、1.5

　　第三题：

　　1、 y=1.6x+11;高为78.2

　　2、 y=-190x+382520;    2008

　　3、 y=7x-21;   12摄氏度

　　4、 y=1/6x-5;   30千克

　　5、 a=1;  k=2,b=-3;  三角形面积3／4

　　6、 当x>2000租用国营出租公司的车合算；每月行驶路程是2000，两家的费用相同;  每月行驶x<2000时，租用个体车合算；  这个单位估计每月行驶的路程在2300千米左右，则租用国营出租公司的车合算.

【初中函数练习题及答案】相关文章：

1.《指数与指数函数》练习题及答案

2.初中力学同步练习题及答案

3.初中《春酒》的练习题及答案

4.初中故乡练习题及答案

5.初中函数应用题及答案

6.函数单元练习题

7.互为反函数的函数图象间的关系练习题及答案参考

8.一次函数练习题带答案