三角函数式的化简

　　化简要求：

　　1）能求出值应求值?

　　2）使三角函数种类最少

　　3）项数尽量少

　　4）尽量使分母中不含三角函数

　　5）尽量不带有根号

　　常用化简方法：

　　线切互化，异名化同名，异角化同角，角的变换，通分，逆用三角公式，正用三角公式。

　　例1、

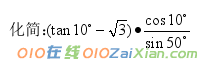
　　三角函数式给值求值：

　　给值求值是三角函数式求值的重点题型，解决给值求值问题关键：找已知式与所求式之间的角、运算以及函数的差异，角的变换是常用技巧，

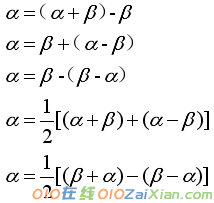
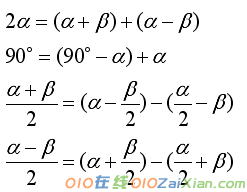
　　给值求值问题往往带有隐含条件，即角的范围，解答时要特别注意对隐含条件的讨论。

　　例2、

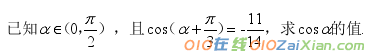
　　三角函数给值求角

　　此类问题是三角函数式求值中的难点，一是确定角的范围，二是选择适当的三角函数。

　　解决此类题的一般步骤是：

　　1）求角的某一三角函数值

　　2）确定角的范围

　　3）求角的值

　　例3.

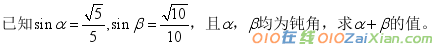
　　总结：

　　解决三角函数式求值化简问题，要遵循“三看”原则：

　　①看角，通过角之间的差别与联系，把角进行合理拆分，尽量向特殊? 角和可计算角转化，从而正确使用公式。

　　②看函数名，找出函数名称之间的差异，把不同名称的等式尽量化成 同名或相近名称的等式，常用方法有切化弦、弦化切。

　　③看式子结构特征，分析式子的结构特征，看是否满足三角函数公式， 若有分式，应通分，可部分项通分，也可全部项通分。

　　“一看角，二看名，三是根据结构特征去变形”